3.1 Position, Displacement, and Average Velocity

Learning Objectives

By the end of this section, you will be able to:

Define position, displacement, and distance traveled.
Calculate the total displacement given the position as a function of time.
Determine the total distance traveled.
Calculate the average velocity given the displacement and elapsed time.

When you’re in motion, the basic questions to ask are: Where are you? Where are you going? How fast are you getting there? The answers to these questions require that you specify your position, your displacement, and your average velocity—the terms we define in this section.

Position

To describe the motion of an object, you must first be able to describe its position (x): where it is at any particular time. More precisely, we need to specify its position relative to a convenient frame of reference. A frame of reference is an arbitrary set of axes from which the position and motion of an object are described. Earth is often used as a frame of reference, and we often describe the position of an object as it relates to stationary objects on Earth. For example, a rocket launch could be described in terms of the position of the rocket with respect to Earth as a whole, whereas a cyclist’s position could be described in terms of where she is in relation to the buildings she passes Figure 3.2. In other cases, we use reference frames that are not stationary but are in motion relative to Earth. To describe the position of a person in an airplane, for example, we use the airplane, not Earth, as the reference frame. To describe the position of an object undergoing one-dimensional motion, we often use the variable x. Later in the chapter, during the discussion of free fall, we use the variable y.

Picture shows three people riding bicycles next to a canal.

Figure 3.2 These cyclists in Vietnam can be described by their position relative to buildings or a canal. Their motion can be described by their change in position, or displacement, in a frame of reference. (credit: modification of work by Suzan Black)

Displacement

If an object moves relative to a frame of reference—for example, if a professor moves to the right relative to a whiteboard Figure 3.3—then the object’s position changes. This change in position is called displacement. The word displacement implies that an object has moved, or has been displaced. Although position is the numerical value of x along a straight line where an object might be located, displacement gives the change in position along this line. Since displacement indicates direction, it is a vector and can be either positive or negative, depending on the choice of positive direction. Also, an analysis of motion can have many displacements embedded in it. If right is positive and an object moves 2 m to the right, then 4 m to the left, the individual displacements are 2 m and $−4$ m, respectively.

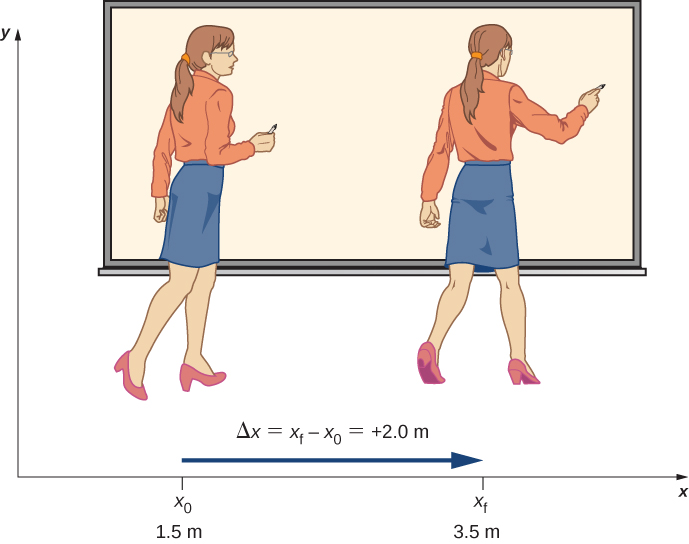
Illustration shows professor at two different locations. The first location is marked as 1.5 meters at the x axis; the second location is marked as 3.5 meters at the x axis. The displacement between the two locations is 2 meters.

Figure 3.3 A professor paces left and right while lecturing. Her position relative to Earth is given by x. The +2.0-m displacement of the professor relative to Earth is represented by an arrow pointing to the right.

Displacement

Displacement $Δ x$ is the change in position of an object:

Δ x = x_{f} - x_{0},

3.1

where $Δ x$ is displacement, $x_{f}$ is the final position, and $x_{0}$ is the initial position.

We use the uppercase Greek letter delta (Δ) to mean “change in” whatever quantity follows it; thus, $Δ x$ means change in position (final position less initial position). We always solve for displacement by subtracting initial position $x_{0}$ from final position $x_{f}$ . Note that the SI unit for displacement is the meter, but sometimes we use kilometers or other units of length. Keep in mind that when units other than meters are used in a problem, you may need to convert them to meters to complete the calculation (see Appendix B).

Objects in motion can also have a series of displacements. In the previous example of the pacing professor, the individual displacements are 2 m and $−4$ m, giving a total displacement of −2 m. We define total displacement $Δ x_{Total}$ , as the sum of the individual displacements, and express this mathematically with the equation

Δ x_{Total} = \sum Δ x_{i},

3.2

where $Δ x_{i}$ are the individual displacements. In the earlier example,

Δ x_{1} = x_{1} - x_{0} = 2 - 0 = 2 m.

Similarly,

Δ x_{2} = x_{2} - x_{1} = −2 - (2) = −4 m.

Thus,

Δ x_{Total} = Δ x_{1} + Δ x_{2} = 2 - 4 = −2 m .

The total displacement is 2 − 4 = −2 m along the x-axis. It is also useful to calculate the magnitude of the displacement, or its size. The magnitude of the displacement is always positive. This is the absolute value of the displacement, because displacement is a vector and cannot have a negative value of magnitude. In our example, the magnitude of the total displacement is 2 m, whereas the magnitudes of the individual displacements are 2 m and 4 m.

The magnitude of the total displacement should not be confused with the distance traveled. Distance traveled $x_{Total}$ , is the total length of the path traveled between two positions. In the previous problem, the distance traveled is the sum of the magnitudes of the individual displacements:

x_{Total} = | Δ x_{1} | + | Δ x_{2} | = 2 + 4 = 6 m .

Average Velocity

To calculate the other physical quantities in kinematics we must introduce the time variable. The time variable allows us not only to state where the object is (its position) during its motion, but also how fast it is moving. How fast an object is moving is given by the rate at which the position changes with time.

For each position $x_{i}$ , we assign a particular time $t_{i}$ . If the details of the motion at each instant are not important, the rate is usually expressed as the average velocity $\overset{–}{v}$ . This vector quantity is simply the total displacement between two points divided by the time taken to travel between them. The time taken to travel between two points is called the elapsed time $Δ t$ .

Average Velocity

If $x_{1}$ and $x_{2}$ are the positions of an object at times $t_{1}$ and $t_{2}$ , respectively, then

\begin{matrix} Average velocity = \overset{–}{v} = \frac{Displacement between two points}{Time needed to make the displacement} \\ \overset{–}{v} = \frac{Δ x}{Δ t} = \frac{x_{2} - x_{1}}{t_{2} - t_{1}} . \end{matrix}

3.3

It is important to note that the average velocity is a vector and can be negative, depending on positions $x_{1}$ and $x_{2}$ .

Example 3.1

Delivering Flyers

Jill sets out from her home to deliver flyers for her yard sale, traveling due east along her street lined with houses. At

0.5

km and 9 minutes later she runs out of flyers and has to retrace her steps back to her house to get more. This takes an additional 9 minutes. After picking up more flyers, she sets out again on the same path, continuing where she left off, and ends up 1.0 km from her house. This third leg of her trip takes

15

minutes. At this point she turns back toward her house, heading west. After

1.75

km and

25

minutes she stops to rest.

What is Jill’s total displacement to the point where she stops to rest?
What is the magnitude of the final displacement?
What is the average velocity during her entire trip?
What is the total distance traveled?
Make a graph of position versus time.

A sketch of Jill’s movements is shown in Figure 3.4.

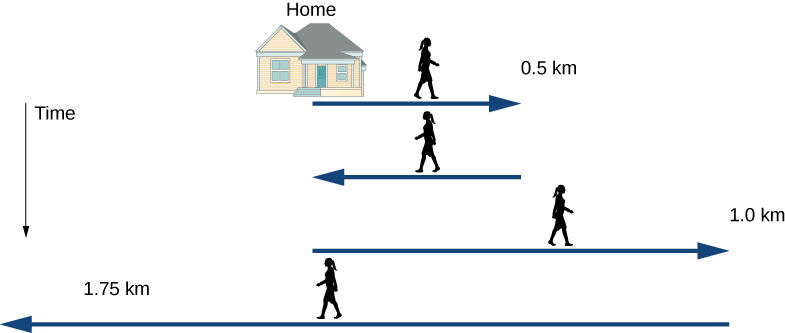
Figure shows a timeline of a person’s movement. First displacement is from the home to the right by 0.5 kilometers. Second displacement is back to the starting point. Third displacement is to the right by 1.0 kilometer. Fourth displacement is from the final point to the left by 1.75 kilometers.

Figure 3.4 Timeline of Jill’s movements.

Strategy

The problem contains data on the various legs of Jill’s trip, so it would be useful to make a table of the physical quantities. We are given position and time in the wording of the problem so we can calculate the displacements and the elapsed time. We take east to be the positive direction. From this information we can find the total displacement and average velocity. Jill’s home is the starting point

x_{0}

. The following table gives Jill’s time and position in the first two columns, and the displacements are calculated in the third column.

Time t_i (min)	Position $x_{i}$ (km)	Displacement $Δ x_{i}$ (km)
$t_{0} = 0$	$x_{0} = 0$	$Δ x_{0} = 0$
$t_{1} = 9$	$x_{1} = 0.5$	$Δ x_{1} = x_{1} - x_{0} = 0.5$
$t_{2} = 18$	$x_{2} = 0$	$Δ x_{2} = x_{2} - x_{1} = −0.5$
$t_{3} = 33$	$x_{3} = 1.0$	$Δ x_{3} = x_{3} - x_{2} = 1.0$
$t_{4} = 58$	$x_{4} = −0.75$	$Δ x_{4} = x_{4} - x_{3} = −1.75$

Solution

From the above table, the total displacement is
$\sum Δ x_{i} = 0.5 - 0.5 + 1.0 - 1.75 km = −0.75 km .$
The magnitude of the total displacement is $| −0.75 | km = 0.75 km$ .
$Average velocity = \frac{Total displacement}{Elapsed time} = \overset{–}{v} = \frac{−0.75 km}{58 min} = −0.013 km/min$
The total distance traveled (sum of magnitudes of individual displacements) is $x_{Total} = \sum | Δ x_{i} | = 0.5 + 0.5 + 1.0 + 1.75 km = 3.75 km$ .
We can graph Jill’s position versus time as a useful aid to see the motion; the graph is shown in Figure 3.5.

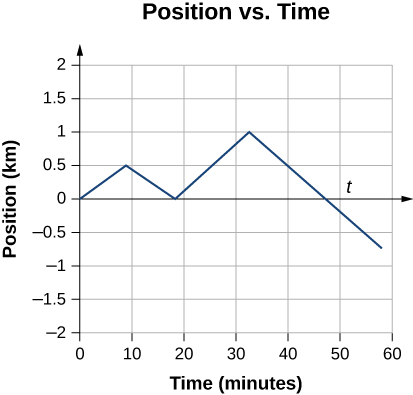Figure 3.5 This graph depicts Jill’s position versus time. The average velocity is the slope of a line connecting the initial and final points.

Significance

Jill’s total displacement is −0.75 km, which means at the end of her trip she ends up

0.75 km

due west of her home. The average velocity means if someone was to walk due west at

0.013

km/min starting at the same time Jill left her home, they both would arrive at the final stopping point at the same time. Note that if Jill were to end her trip at her house, her total displacement would be zero, as well as her average velocity. The total distance traveled during the 58 minutes of elapsed time for her trip is 3.75 km.

Python Skill

Functions

Now that we are talking about position as a function of time, we will introduce how to represent a mathematical function in Python. We will not go into all the details about all that functions in Python can do, but we will describe how they can be used to represent mathematical functions. Suppose we have the mathematical function $f (x) = 3 x - 2$ . The way we represent that in Python is shown below. Once we have a function, we can give any input and the code will return the output of the function. In the example below, we first define a function, and they we use it by plugging in a specific value of $x$ .

# define the function first def f(x): return 3*x - 2 # use the function at a specific value x = 2.0 specific_value = f(2.0) print(specific_value)

Instead of just using an equal sign, Python expects the function expression to be in a new indented line. The indent should be 4 spaces. The def tells Python that we are defining a function. Then we give the name of the function. The name of a function can be a whole word but we will often just use a letter. (This is the same as the way we name variables.) The value inside the parenthesis then gives what the input variable is. Here our function took $x$ as the input, but often in physics time will be the input. Remember to put a colon after the closing parenthesis. The return aregument tells Python what the function is going to output, so for our use we will put the mathematical expression right after the return argument.

When we are ready to use the function, we put the name of the function, and then input the specific value of $x$ that we want.

Now let's look at a more physical example. Suppose the postion as a function of time is given as $x (t) = 3 t - 2$ . We want to find the value of the position when $t = 2.0$ . This is done in the code below.

# define the function first def x(t): return 3*t - 2 # use the function at a specific value t = 2.0 specific_value = x(2.0) print(specific_value)

While this may seem like more to type in for something that we could quickly calculate, functions can be powerful when we need to plug in a large number of different inputs. They can also be useful for organizing our work into something that is either more meaningful or more computationally efficient.

In many of our examples in this text, we will try to use Python functions to represent our mathematical functions as given in the problem statement. That way if we want to modify the code to apply to a new problem, the place to change should be more easily identafiable.

Code Example 3.1

Suppose we have a particle whose position is given as a function of time $x (t) = \sin (2 t) + \frac{1}{2} t$ . We can use python to visualize how the particle will move throughout time. Because we have a position function of time, we will use a function to make this plot. Luckily for us, the linspace array of our time values can be inputted into our function, and the output will be an array of all the individual outputs.

from matplotlib import pyplot as plt # import plotting function from numpy import linspace, sin # this function creates equally spaced t points # define function def x(t): return sin(2*t) + (1/2)*t tpoints = linspace(0, 8, 100) # create 100 points from 0 to 8 seconds. xpoints = x(tpoints) # put tpoints array into function # plot the results plt.clf() plt.plot(tpoints, xpoints) plt.xlabel('Time (s)') plt.ylabel('Position (m)') plt.title('Position vs Time Graph') plt.show()

Now suppose we have a second particle whose position is given with the new function $x (t) = \frac{t^{2}}{2} - 3 t + 2$ . We want to find the time(s) where these two particles are at the same place. We can add this new function to our plot as shown.

from matplotlib import pyplot as plt # import plotting function from numpy import linspace, sin # this function creates equally spaced t points # definet the two functions def x1(t): return sin(2*t) + (1/2)*t def x2(t): return (1/2)*t**2 - 3*t + 2 tpoints = linspace(0, 8, 100) # create 100 points from 0 to 8 seconds. xpoints = x1(tpoints) # put tpoints array into function xpoints2 = x2(tpoints) # plot the results plt.clf() plt.plot(tpoints, xpoints, label='1st Particle') plt.plot(tpoints, xpoints2, label='2nd Particle') plt.legend() # add a legend plt.xlabel('Time (s)') plt.ylabel('Position (m)') plt.title('Position vs Time Graph') plt.show()

By plotting both of the position vs time graphs for each particle, we can see that the two particles will be at the same place at about 0.5 seconds, and at about 6.5 seconds.

Check Your Understanding 3.1

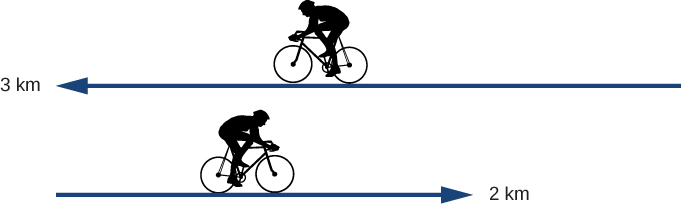
A cyclist rides 3 km west and then turns around and rides 2 km east. (a) What is their displacement? (b) What is the distance traveled? (c) What is the magnitude of their displacement?

Figure shows timeline of cyclist’s movement. First displacement is to the left by 3.0 kilometers. Second displacement is from the final point to the right by 2.0 kilometers.